
Sia

Question
Math
Posted over 1 year ago
Region is enclosed by the curve and the line .
What is the volume of the solid generated when is rotated about the axis?
Give an exact answer in terms of .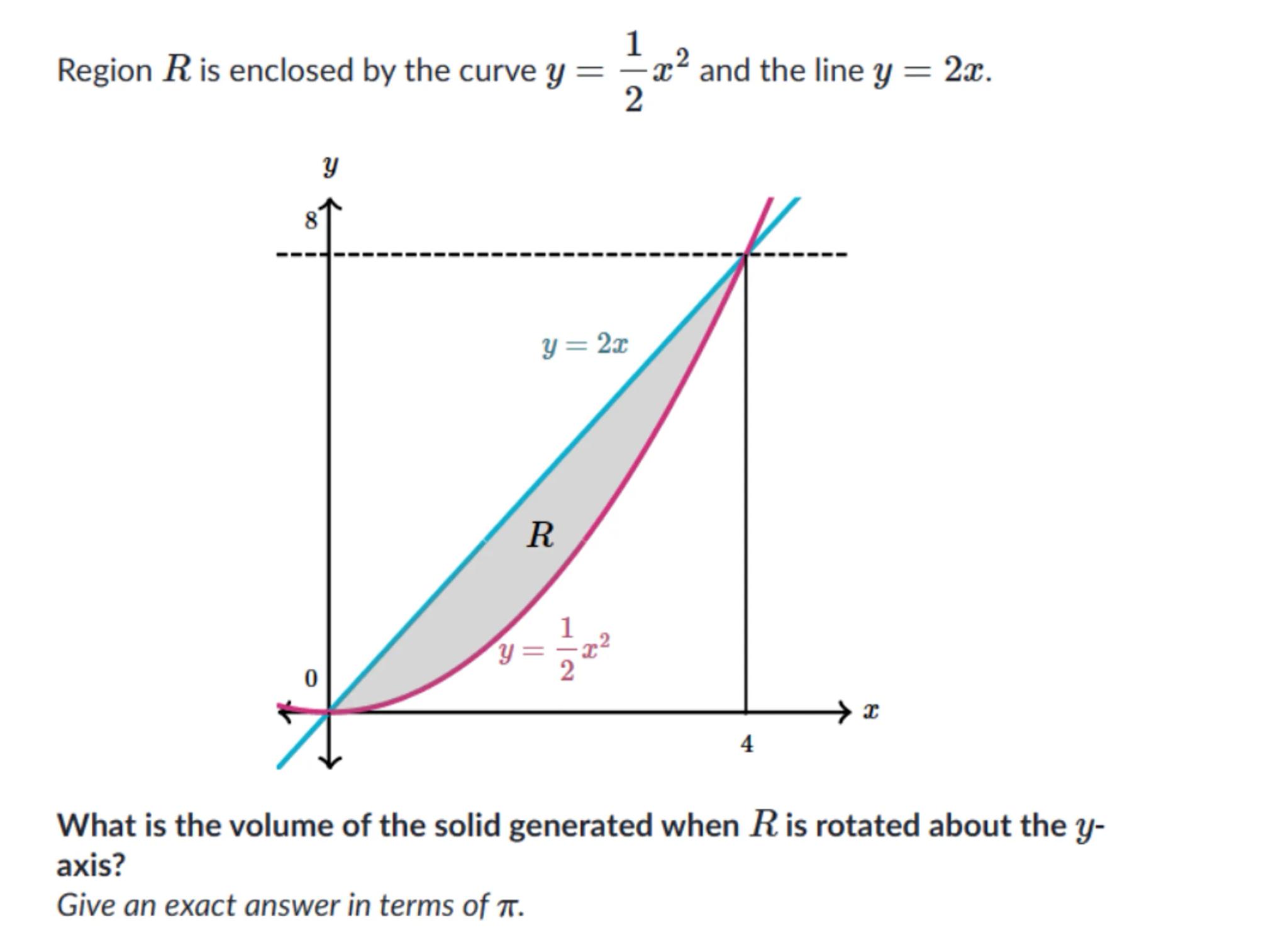

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the volume of the solid generated when region is rotated about the -axis, we use the method of cylindrical shells. The volume is given by the integral formula:
where is the height of the shell and is the radius
step 2
The region is enclosed by the curves and . We need to find the points of intersection to determine the limits of integration. Setting , we solve for :
Thus, and
step 3
The volume integral becomes:
Simplifying the integrand:
step 4
We now integrate term by term:
step 5
Compute the integrals:
step 6
Substitute back into the volume formula:
Answer
The exact volume of the solid generated when region is rotated about the -axis is .
Key Concept
Volume of solid of revolution using cylindrical shells
Explanation
The volume is calculated by integrating the product of the radius and height of cylindrical shells formed by rotating the region around the -axis.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question