
Sia
!
Required information
Block supports a pipe column and rests as shown on wedge . The coefficient of static friction at all surfaces of contact is 0.25 and that . Assume the wedges are massless.
Determine the smallest force P required to raise block .
Given: .
The smallest force required to raise block is .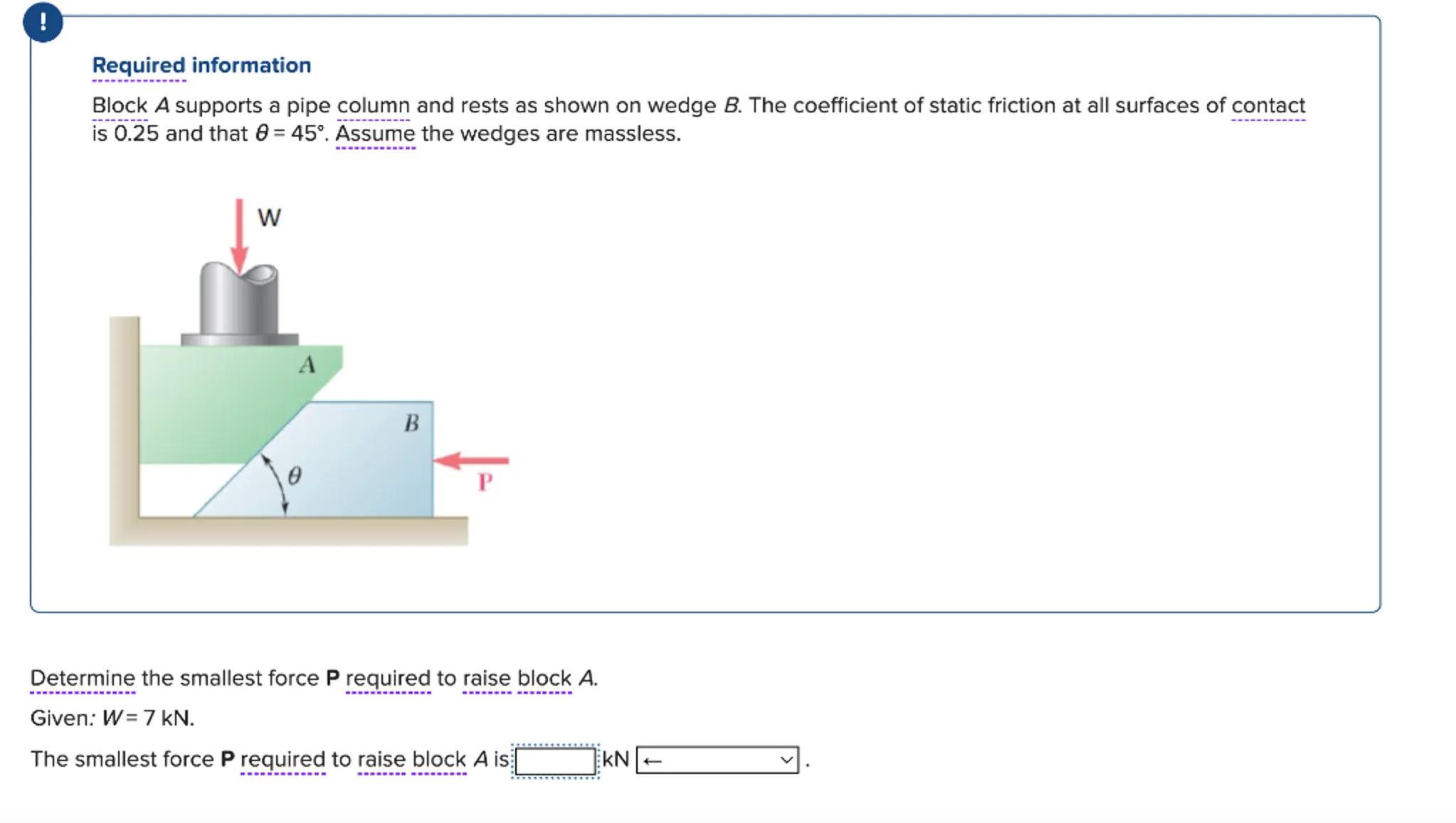

Answer from Sia
Posted about 1 year ago
Solution
a
Start by analyzing the forces acting on block A. The weight of block A is given as acting downward. The static friction force, which opposes the motion, can be expressed as , where is the coefficient of static friction and is the normal force exerted by wedge B on block A. Since the wedge is massless, the normal force is equal to the vertical component of the force exerted by the wedge
b
The normal force can be resolved into components. The vertical component of the force due to the weight of block A is , and the horizontal component is influenced by the applied force . The angle is given as , so we can express the normal force as . The vertical equilibrium condition gives us: . Substituting for , we have:
c
Since , we can simplify the equation to: , which leads to: . Therefore, we find that
Answer
14 kN
Key Concept
Static Equilibrium: In static equilibrium, the sum of forces acting on an object must be zero. This includes resolving forces into their components and applying the conditions for equilibrium. The frictional force is also a key factor in determining the forces required to maintain equilibrium.
Explanation
The smallest force P required to raise block A is determined by balancing the forces acting on it, considering both the weight and the frictional forces involved. By applying the equilibrium conditions, we find that P must be 14 kN to overcome the weight of block A.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question