
Sia

Question
Biology
Posted over 1 year ago
The bacterium Bacillus symbiodinium has a generation time of 20 minutes. Starting with one cell in log phase, how many minutes does it take to produce about 1,000 cells ? Assume all cells remain viable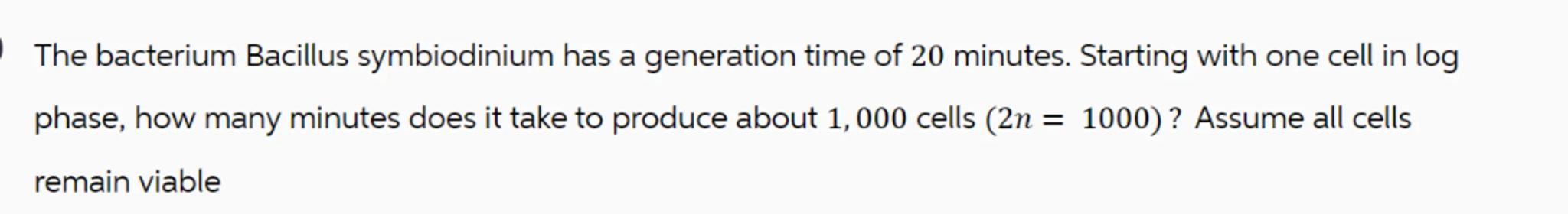

Answer from Sia
Posted over 1 year ago
Answer
It takes 200 minutes to produce about 1,000 cells from one cell of Bacillus symbiodinium.
Solution
a
Determine the number of generations required to reach 1,000 cells: Use the formula to find n
b
Calculate the number of generations: Solving for n gives . Since we cannot have a fraction of a generation, we round up to 10 generations
c
Calculate the total time: Multiply the number of generations by the generation time. For Bacillus symbiodinium, the generation time is 20 minutes, so minutes
Key Concept
Generation time and exponential growth
Explanation
The generation time is the time it takes for a population to double. Bacterial growth can be modeled exponentially, and the time to reach a certain population size can be calculated by determining the number of generations required and multiplying by the generation time.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question