
Sia

Question
Chemistry
Posted over 1 year ago
The diffusion coefficient of is and that for is . If a solution of gives a diffusion current of , what will be the diffusion current for a solution of using the same polarographic cell?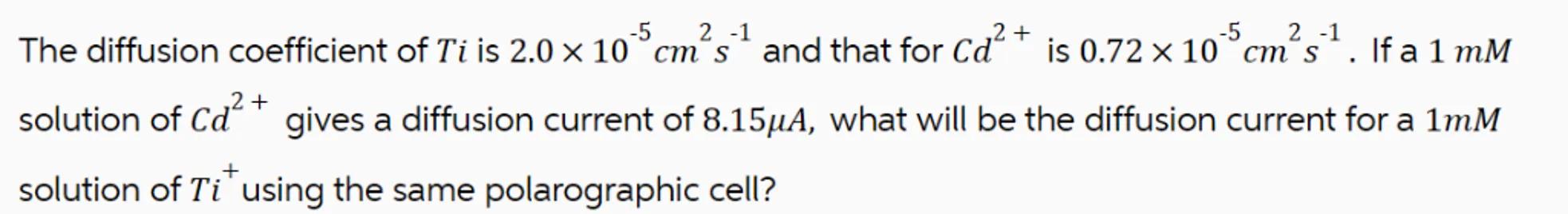

Answer from Sia
Posted over 1 year ago
Solution
1
Identify the given data: The diffusion coefficient of is and that for is . The diffusion current for a solution of is
2
Use the Ilkovic equation: The Ilkovic equation relates the diffusion current () to the diffusion coefficient (), concentration (), and other constants. The equation is , where is a constant, is the number of electrons transferred, and is the Faraday constant
3
Set up the ratio: Since the same polarographic cell is used, , , and are constants and can be canceled out. The ratio of the diffusion currents for and can be expressed as
4
Calculate the ratio: Substitute the given diffusion coefficients into the ratio:
5
Solve for $i_{d, Ti^+}$: Calculate the square roots and solve for : . Therefore,
Answer
The diffusion current for a solution of is approximately .
Key Concept
The Ilkovic equation relates diffusion current to the diffusion coefficient and concentration.
Explanation
By using the ratio of the diffusion coefficients and the given diffusion current for , we can calculate the diffusion current for .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question