
Sia
The graph below represents the distribution of molecular speeds of hydrogen and neon at .
1. Match each curve to the appropriate gas.
2. Calculate the rms speed (in ) for each of the gases at .
3. Which of the gases would you expect to have the greater effusion rate at ? Justify your answer.
4. Calculate the temperature at which the rms speed of the hydrogen gas would equal the rms speed of the neon at .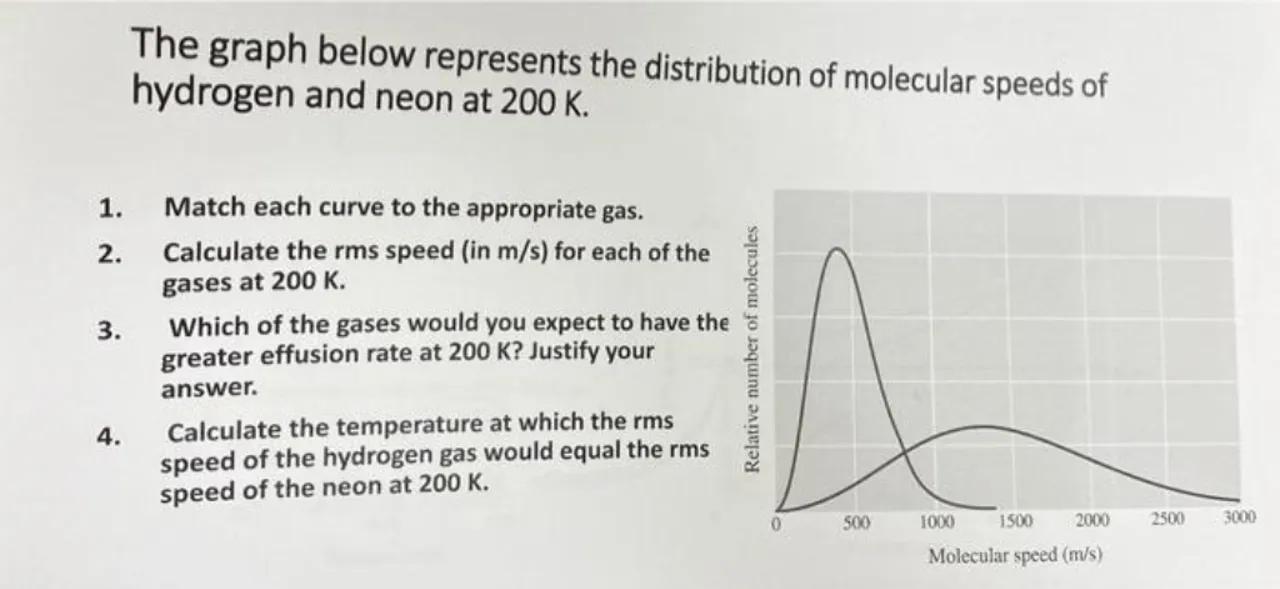

Answer from Sia
Posted over 1 year ago
For question 1:
A
Key Concept
Molecular mass and speed distribution
Explanation
The curve for hydrogen is taller and narrower because hydrogen has a lower molecular mass than neon, leading to a higher proportion of molecules with higher speeds at the same temperature.
For question 2:
B
Key Concept
Root-mean-square (rms) speed
Explanation
The rms speed can be calculated using the formula , where is the Boltzmann constant, is the temperature, and is the molar mass of the gas.
For question 3:
C
Key Concept
Graham's law of effusion
Explanation
Hydrogen will have a greater effusion rate than neon at the same temperature because the rate of effusion is inversely proportional to the square root of the molar mass of the gas.
For question 4:
D
Key Concept
Equating rms speeds for different temperatures
Explanation
To find the temperature at which hydrogen has the same rms speed as neon at 200 K, set the rms speed equations equal to each other and solve for the new temperature of hydrogen.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
