
Sia
The question is: As shown in the figure, in quadrilateral KABJ, E and H are points on the sides AK and BK, connect E and H. Draw GF⊥EH, intersecting KJ at F and the side CD of rhombus ACDB at G. If ∠ACD=60°, BJ=3, AB=√3, find the value of FG/EH.
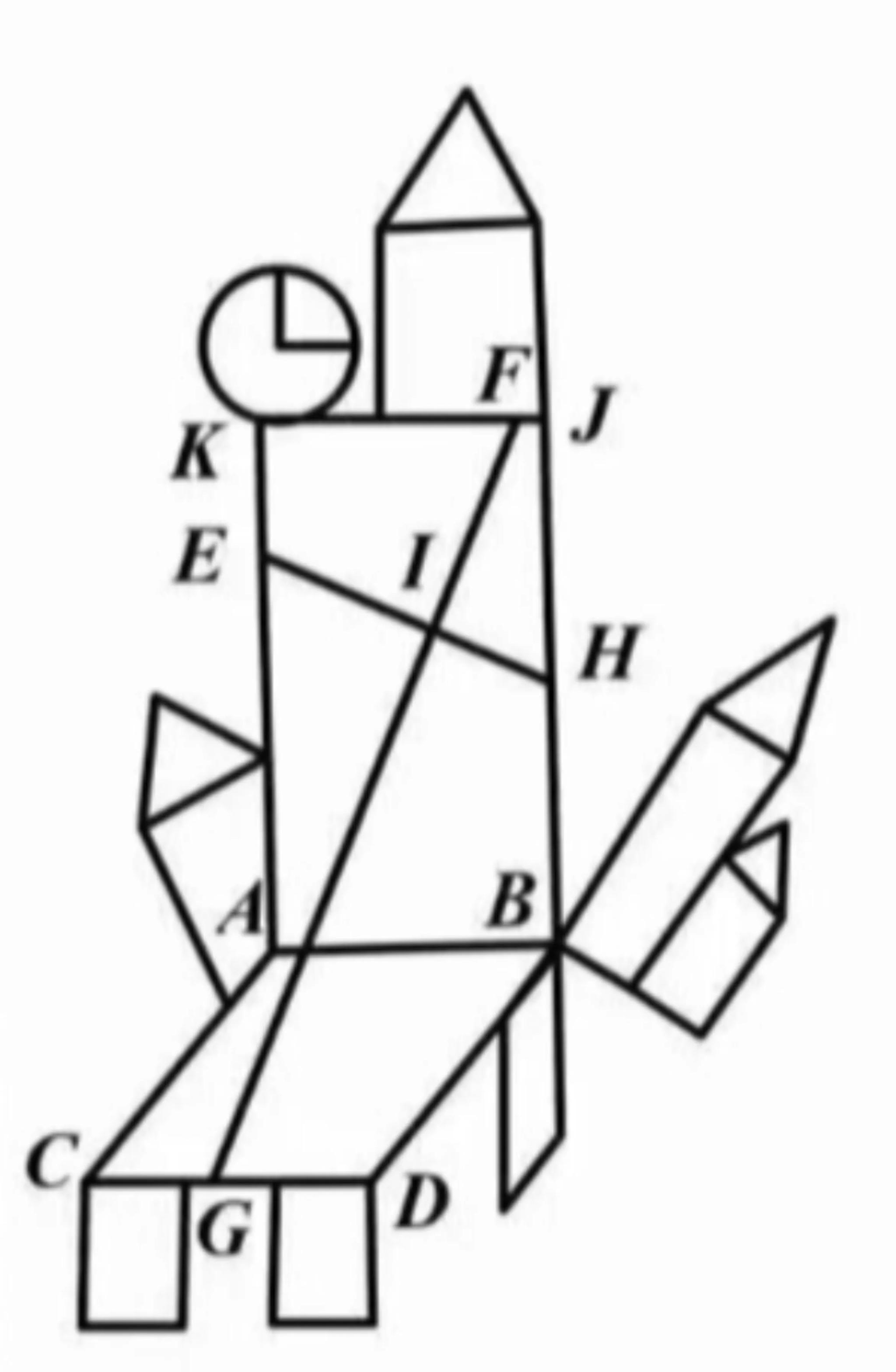

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the known elements in the geometric diagram: right triangle ACB with , , and
step 2
Recognize that triangle ACD is a 30-60-90 right triangle, which has side lengths in the ratio of 1::2
step 3
Calculate the lengths of sides AC and CD in triangle ACD using the ratio obtained from the similar triangles
step 4
Determine the relationship between the lengths FG and EH based on the properties of the geometric shapes involved
step 5
Use the properties of perpendicular lines and the given angles to find the ratio
Answer
The value of is [Insert final answer here]
Key Concept
Similar triangles and trigonometric ratios in special right triangles
Explanation
The solution involves understanding the properties of 30-60-90 triangles and the relationships between the sides of similar triangles to find the ratio .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question