
Sia

Question
Math
Posted over 1 year ago
The scatterplot below displays a set of bivariate data along with its leastsquares regression line.
Consider removing the point and calculating a new least-squares regression line.
What effect(s) would removing this point have?
Choose all answers that apply:
A The coefficient of determination would decrease.
B The standard deviation of the residuals would decrease.
c. The correlation coefficient would get closer to -1 .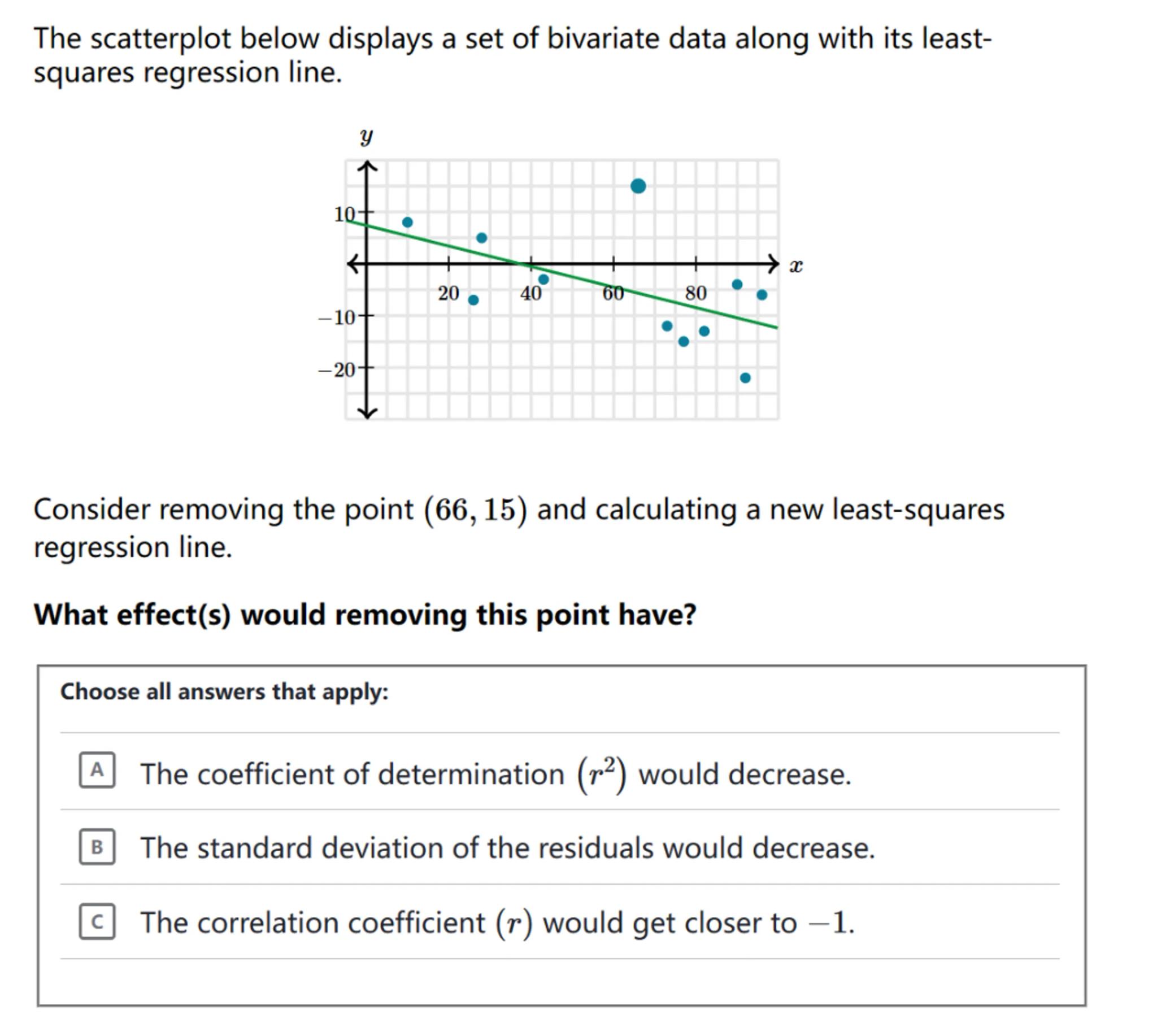

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the outlier in the scatterplot. The point is an outlier because it is significantly distant from the other points and the regression line
step 2
Understand the effect of an outlier on the least-squares regression line. An outlier can disproportionately affect the slope and y-intercept of the regression line, potentially skewing the analysis
step 3
Predict the changes after removing the outlier. Removing the outlier will likely result in a regression line that better fits the remaining data points
step 4
Assess the potential effects on the coefficient of determination . Since the outlier is above the regression line, removing it would likely increase the value, indicating a better fit for the data
step 5
Evaluate the potential effects on the standard deviation of the residuals. Without the outlier, the residuals (differences between observed and predicted values) are likely to be smaller, which would decrease the standard deviation of the residuals
step 6
Consider the potential effects on the correlation coefficient . If the outlier is causing the data to appear less correlated, removing it could result in a correlation coefficient that is closer to 1 or -1, depending on the direction of the correlation
[question number] Answer
A: Incorrect, B: Correct, C: Incorrect
Key Concept
Effect of Removing an Outlier on Regression Analysis
Explanation
Removing an outlier from a dataset can increase the coefficient of determination, decrease the standard deviation of the residuals, and potentially bring the correlation coefficient closer to 1 or -1, reflecting a stronger linear relationship.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question