
Sia

Question
Math
Posted over 1 year ago
The theater director offered every member of the drama one vote for which play they preferred to perform. The director found that voted for The Oddems Family, that voted for Thirteenth Night, and that did not vote.
In this group, are the events "Oddems Family" and "Thirteenth Night" mutually exclusive?
Choose 1 answer:
(A) Yes
(B) No
Find the probability that a randomly selected person from this group voted for Oddems Family OR Thirteenth Night.
Oddems Family OR Thirteenth Night 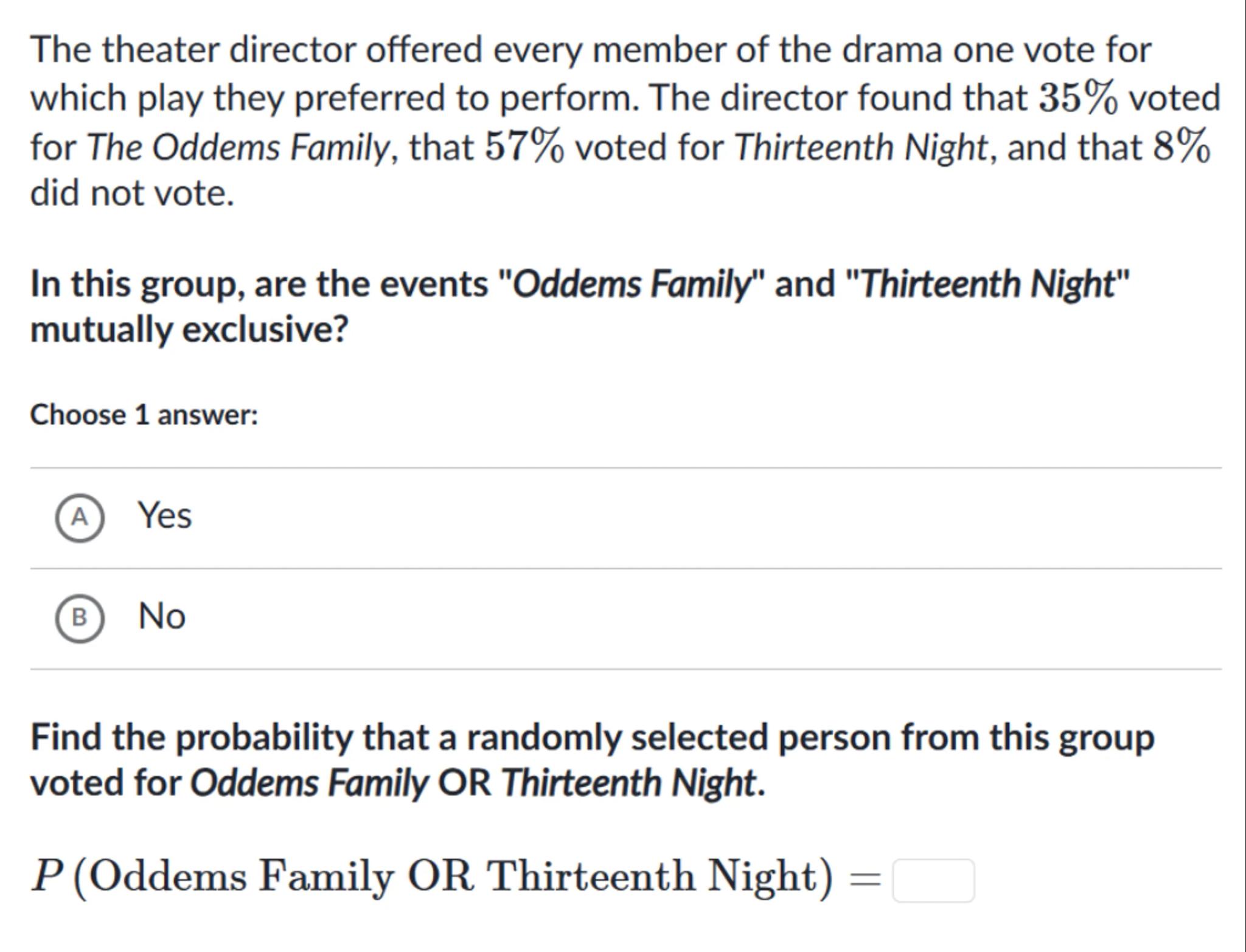

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To determine if the events "Oddems Family" and "Thirteenth Night" are mutually exclusive, we need to check if the sum of their probabilities exceeds 100%
step 2
The probability of voting for "Oddems Family" is 35%, and for "Thirteenth Night" is 57%
step 3
Adding the probabilities:
step 4
Since the sum of the probabilities is less than 100% and there is a percentage of people who did not vote, the events can be considered mutually exclusive
step 5
To find the probability that a person voted for either "Oddems Family" OR "Thirteenth Night", we add the probabilities of the two events
step 6
Calculating the probability:
1 Answer
(A) Yes, the events are mutually exclusive.
.
Key Concept
Mutual Exclusivity and Addition Rule in Probability
Explanation
Events are mutually exclusive if they cannot occur at the same time. The addition rule states that the probability of either event occurring is the sum of their individual probabilities, provided the events are mutually exclusive.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question