
Sia
Use the Gaussian elimination method to solve the system of linear equations. If the system has infinitely many solutions, write the solution set with z arbitrary.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. There is one solution. The solution is .
(Simplify your answers. Type integers or decimals.)
B. There are infinitely many solutions. The solutions are , where is any real number. (Simplify your answers. Type integers or decimals.)
C. The system is inconsistent. The solution set is .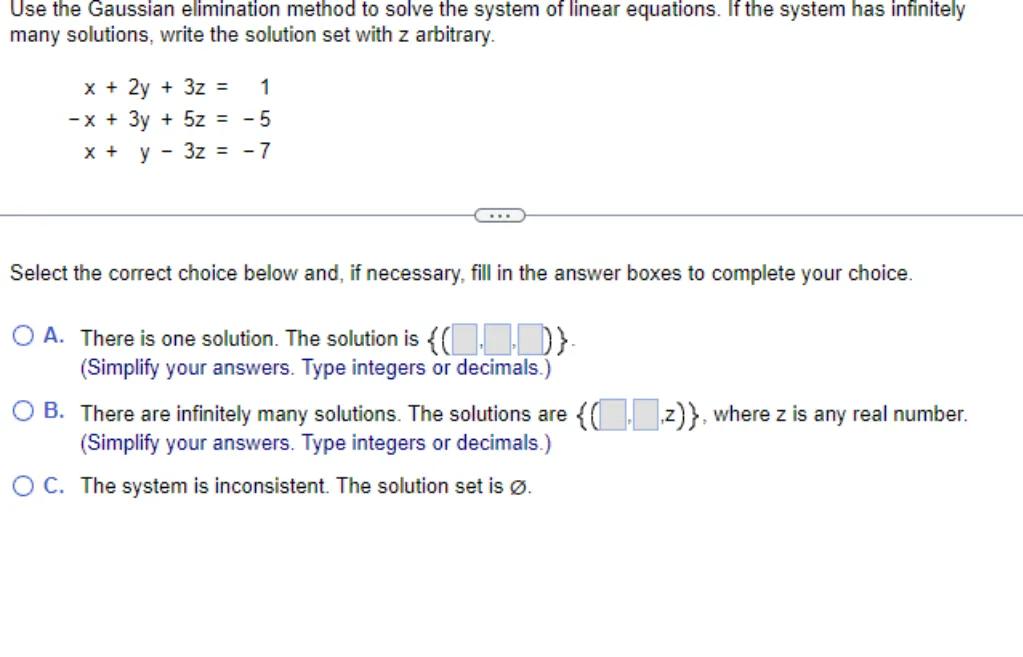

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
We can represent the system in augmented matrix form:
step 3
We perform row operations to reach reduced row echelon form. First, we can replace Row 2 with Row 2 + Row 1:
step 4
Next, we replace Row 3 with Row 3 - Row 1:
step 5
We can simplify Row 2 and Row 3 further to isolate variables, leading to the conclusion that the system has infinitely many solutions expressed as:
B
Key Concept
Gaussian elimination and row operations
Explanation
This method allows us to systematically solve systems of linear equations by transforming the augmented matrix into a simpler form, revealing the relationships between the variables.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question