Asksia AI LOGO

Sia

Question
Statistics
Posted 7 months ago

Use the figure shown to answer the question.
Two supply curves

According to each supply curve, what quantities would be produced at $30\$ 30 ?

Choose 1 answer:
(A) \begin{tabular}{|ll|} \hlineQSQ_{S} on S1S_{1} & QSQ_{S} on S2S_{2} \\ \hline 30 & 30 \\ \hline \end{tabular}
(B) \begin{tabular}{|ll} \hlineQSQ_{S} on S1S_{1} & QSQ_{S} on S2S_{2} \\ \hline 30 & 10 \end{tabular}
(c) \begin{tabular}{ll|} \hlineQSQ_{S} on S1S_{1} & QSQ_{S} on S2S_{2} \\ \hline 0\mathbf{0} & 0\mathbf{0} \end{tabular}
(D) \begin{tabular}{|ll|} \hlineQSQ_{S} on S1S_{1} & QSQ_{S} on S2S_{2} \\ \hline 0 & 30 \end{tabular}
(E) \begin{tabular}{ll} QSQ_{S} on S1S_{1} & QSQ_{S} on S2S_{2} \\ \hline 40 & 0 \end{tabular}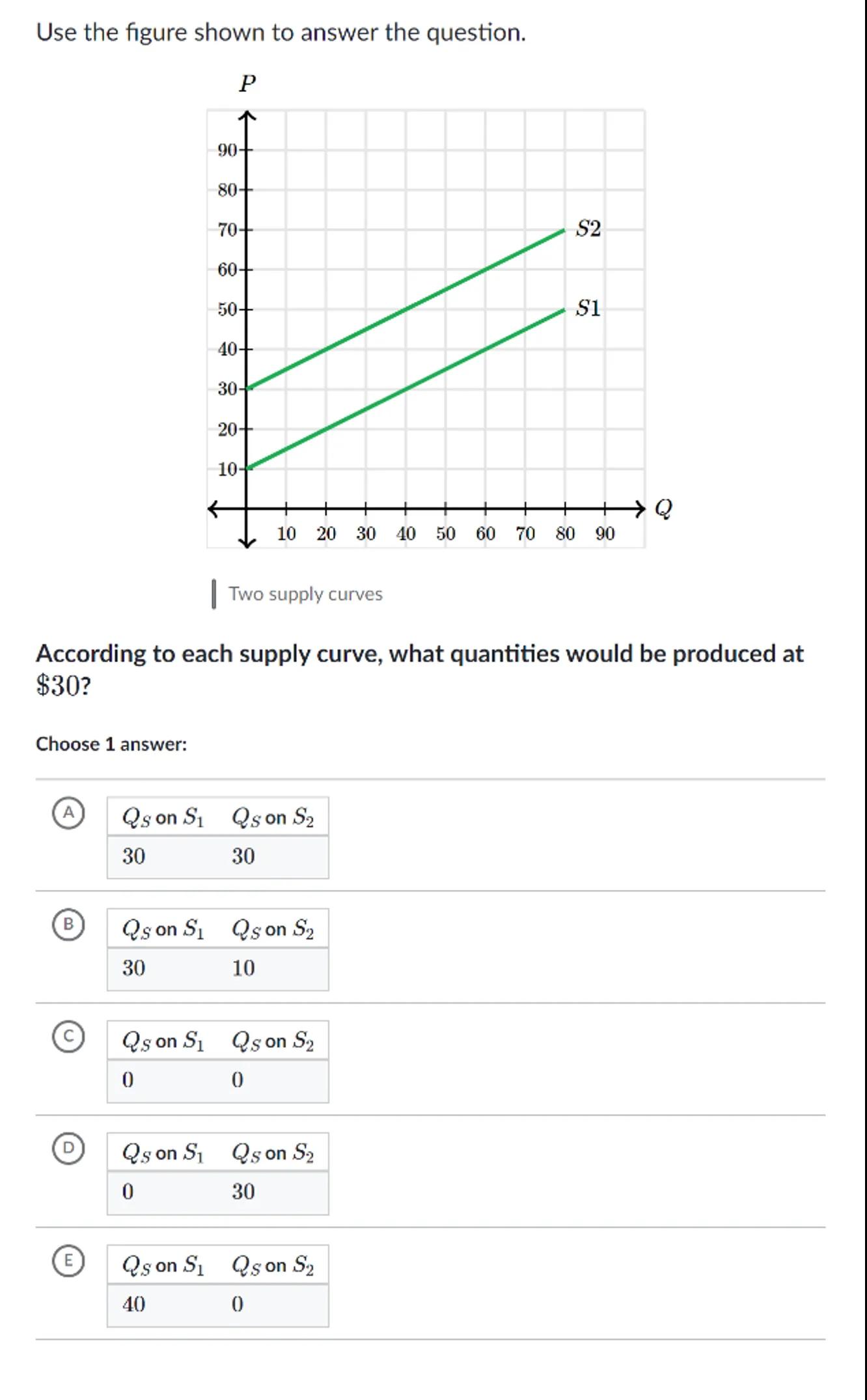
Sign in to unlock the answer
Answer from Sia
Posted 7 months ago
Solution by Steps
step 1
To determine the quantity produced at a price of 30onsupplycurveS1,weneedtofindthepointonthelineS1thatcorrespondstoaprice(P)of30 on supply curve S1, we need to find the point on the line S1 that corresponds to a price (P) of 30
step 2
Using the two points given for S1, (0,10) and (80,60), we can find the slope of the line using the formula m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
step 3
Substituting the points into the slope formula: m=60−1080−0=5080=58m = \frac{60 - 10}{80 - 0} = \frac{50}{80} = \frac{5}{8}
step 4
With the slope m=58m = \frac{5}{8} and the point (0,10), we can use the point-slope form of the equation of a line, y−y1=m(x−x1)y - y_1 = m(x - x_1), to find the equation of S1
step 5
Substituting the slope and point into the point-slope form: P−10=58(Q−0)P - 10 = \frac{5}{8}(Q - 0), which simplifies to P=58Q+10P = \frac{5}{8}Q + 10
step 6
To find the quantity produced at P=P = 30 on S1, we substitute P=30P = 30 into the equation: 30=58Q+1030 = \frac{5}{8}Q + 10
step 7
Solving for QQ: 30−10=58Q30 - 10 = \frac{5}{8}Q, which simplifies to 20=58Q20 = \frac{5}{8}Q
step 8
Multiplying both sides by 85\frac{8}{5} to isolate QQ: Q=85×20=32Q = \frac{8}{5} \times 20 = 32
step 9
To determine the quantity produced at a price of 30onsupplycurveS2,weneedtofindthepointonthelineS2thatcorrespondstoaprice(P)of30 on supply curve S2, we need to find the point on the line S2 that corresponds to a price (P) of 30
step 10
Using the two points given for S2, (0,30) and (80,70), we can find the slope of the line using the formula m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
step 11
Substituting the points into the slope formula: m=70−3080−0=4080=12m = \frac{70 - 30}{80 - 0} = \frac{40}{80} = \frac{1}{2}
step 12
With the slope m=12m = \frac{1}{2} and the point (0,30), we can use the point-slope form of the equation of a line, y−y1=m(x−x1)y - y_1 = m(x - x_1), to find the equation of S2
step 13
Substituting the slope and point into the point-slope form: P−30=12(Q−0)P - 30 = \frac{1}{2}(Q - 0), which simplifies to P=12Q+30P = \frac{1}{2}Q + 30
step 14
To find the quantity produced at P=P = 30 on S2, we substitute P=30P = 30 into the equation: 30=12Q+3030 = \frac{1}{2}Q + 30
step 15
Solving for QQ: 30−30=12Q30 - 30 = \frac{1}{2}Q, which simplifies to 0=12Q0 = \frac{1}{2}Q
step 16
Since 0=12Q0 = \frac{1}{2}Q, the quantity produced at P=P = 30 on S2 is Q=0Q = 0
Answer
The quantities produced at a price of $30 are 32 units on supply curve S1 and 0 units on supply curve S2.
B
Key Concept
Interpreting supply curves
Explanation
To find the quantity supplied at a given price, locate the price on the y-axis and find the corresponding quantity on the x-axis where the price level intersects the supply curve.

Not the question you are looking for? Ask here!

Enter question by text

Enter question by image

Unlock Smarter Learning with AskSia Super!

Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.

30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question