
Sia

Question
Math
Posted over 1 year ago
What is the general solution to the differential equation that generated the slope field?
Choose 1 answer:
(A)
(B)
(C)
(D)
(E) 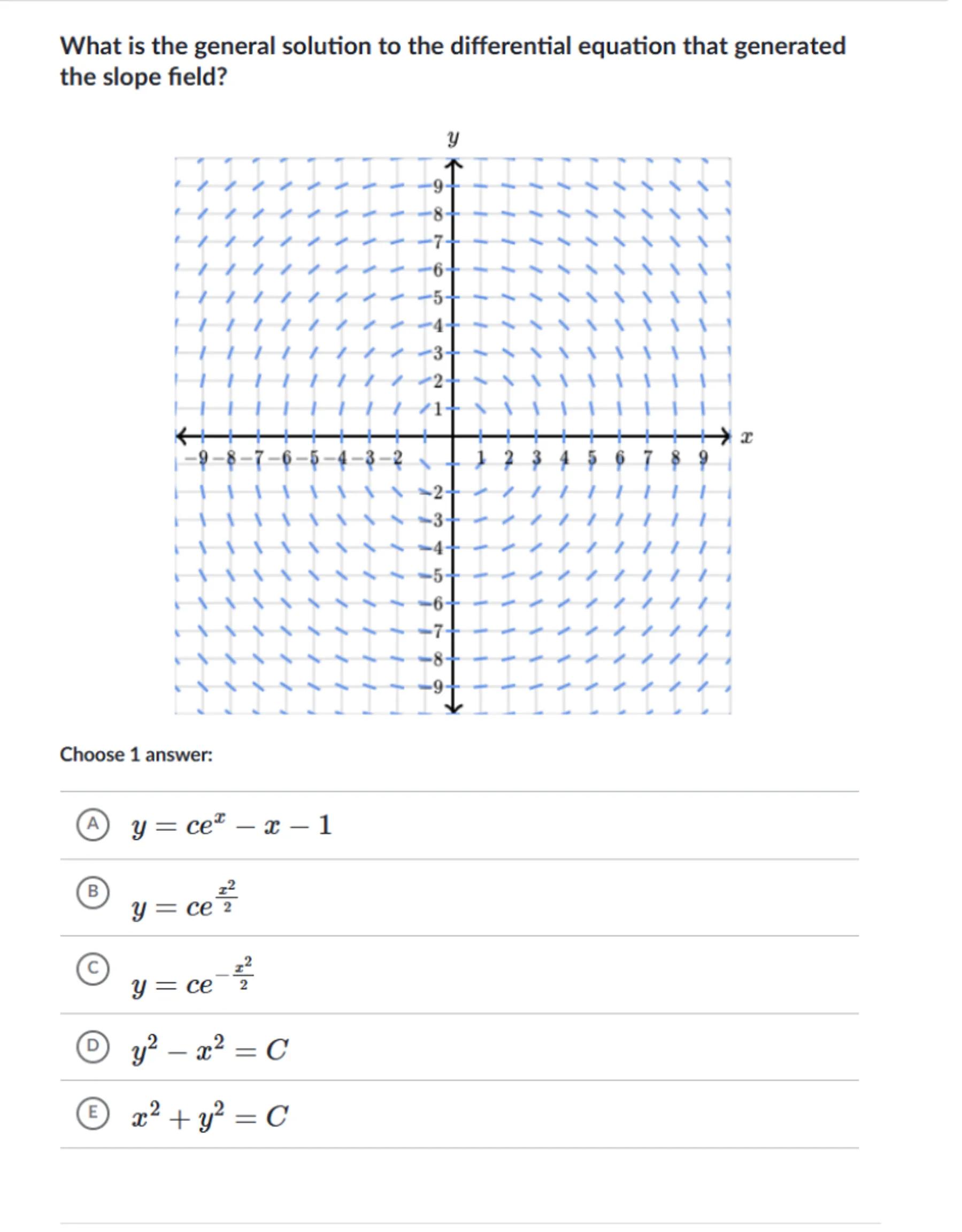

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The slope field shows that the slopes are steeper in the top left and bottom right corners, and flatter in the top right and bottom left corners. This suggests a relationship involving and
step 3
Option (D) and Option (E) both involve and
step 4
The slope field does not suggest a circular symmetry, which would be the case for
step 5
Therefore, the correct general solution that matches the slope field is
D
Key Concept
Differential Equation Solution
Explanation
The slope field's characteristics suggest a hyperbolic relationship, which matches the form .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question