
Sia

Question
Math
Posted over 1 year ago
.
What is the length of ?
Round to one decimal place.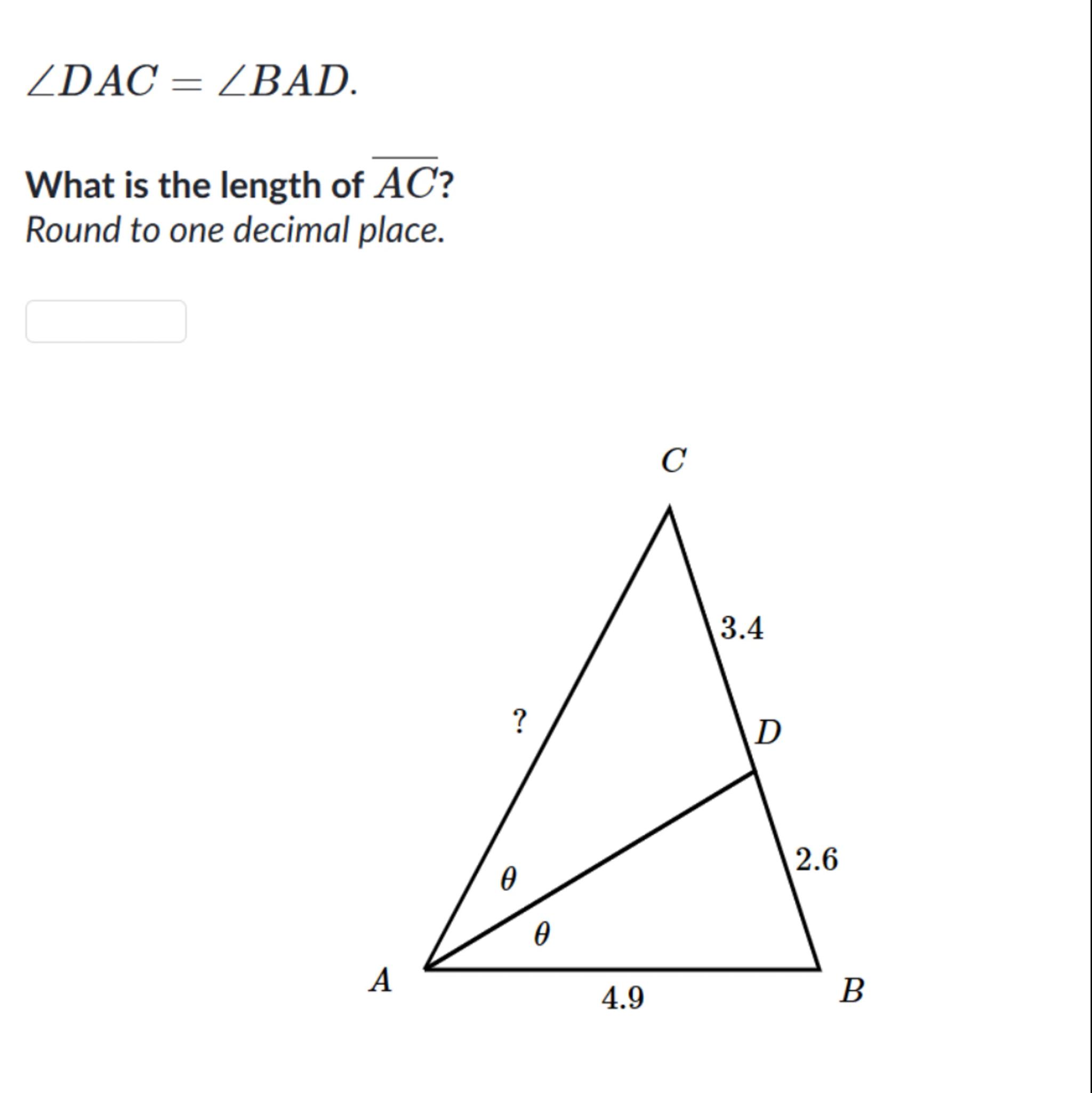

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Given that , we can conclude that and are similar by the Angle-Angle (AA) criterion for similarity
step 2
To find the length of , we set up a proportion using corresponding sides from the similar triangles and
step 3
The proportion is . Substituting the given lengths, we get
step 4
We also know that
step 5
Substituting into the proportion, we get
step 6
To solve for , cross-multiply to get
step 7
Simplifying, we find
step 8
Calculating the value, we get when rounded to one decimal place
Answer
The length of is approximately 7.3 units.
Key Concept
Similar Triangles and Proportions
Explanation
The length of was found by using the properties of similar triangles to set up a proportion between corresponding sides and solving for the unknown length.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question